The Downfall of Headphone Jacks
As you can tell by the title of this post, I am pretty upset about
Prerequisite knowledge:
https://projecteuclid.org/download/pdf_1/euclid.aop/1176988613
Just kidding, here are videos for you to watch about the topic.
https://www.youtube.com/watch?v=ZWib5olGbQ0 Numberphile
https://www.youtube.com/watch?v=OeJobV4jJG0 Vsauce2
Oh, you’re too lazy to watch that video too? Well I suppose I could give an explanation.
The Optimal Stopping Problem
Say you had a bunch of things to choose from, and you want the best possible one.
Let’s talk ang paos.
Say you had a bunch of ang paos with a random amount of money in each one. You also have a lot of siblings who also want those ang paos. You, being the oldest one get first pick. You can open each one and check how much there is inside, then decide to keep it or move to the next one.
The catch is: once you move to the next one, your siblings immediately take it and you can’t have it anymore. If you look through every one, you will only be able to pick the last one.
The problem is, how do you get the one with the most amount of money?
To rephrase the question, how do you know when to stop opening, and start choosing?
This is known as the optimal stopping problem.
Some very smart and bored people came up with a solution to this, and you can watch the explanations in the videos linked above. The idea is that, you will first look through a subset of ang paos. The magic number is $1 \over e$, or about 37%. Once you do that, you will have an idea of what the rough distribution of values is. You then pick the next one that is the higher than those seen before.
If you are interested in the math behind this, again, the links are above.
A worked example
Say you have 10 ang paos. We know that our optimal stopping point is after $\lceil\frac{10}{e}\rceil = 4$.
So we open 4 ang paos to get our sample. You now just need to choose the next one that’s higher than 54, whatever that may be.
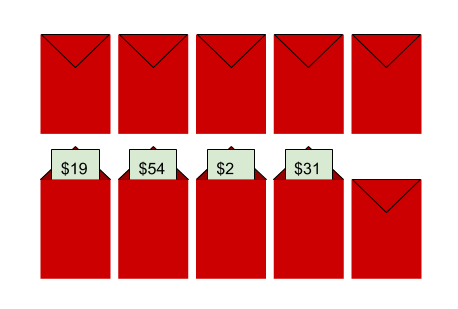
Surprisingly, by doing this, your chances of getting the highest possible value is approximately 1 in 3*. Considering that if you picked the items at random, your chances would be 1 in 10, this is quite a large improvement. And this doesn’t change no matter how many ang paos you have. You could have 100 or 92,018,502,993,850,205** ang paos and you would still have a 1 in 3 chance of getting the highest number.
* Working under the assumption that we’re working with a random distribution.
** That's ninety two quadrillion ,
eighteen trillion ,
five hundred two billion ,
nine hundred ninety three million ,
eight hundred fifty thousand ,
two hundred five for those wondering
Note: This is indeed an O(n) algorithm, and you'd probably be dead before you could check all those ang paos.
Life is short
We can apply this concept seeking a relationship.
I only get 8 shots.
Say I start dating at 19 years old. And I really want to stop dating by the time I’m 35.
That gives me 16 good years of dating. Based on current data, I have an average of one new relationship every 2-ish years. (I’m not enough of a player to achieve more than that and I don’t actively go out to seek new potential soulmates) That results in 8 relationships in my lifetime given my current parameters.
The optimal way of doing this would be to go through all 8 relationships and then choose the best one for myself. But due to societal pressures and inconsistent and ever changing data, we are unable to apply the stable marriage algorithm to this problem. We’re left with no choice but to apply the optimal stopping algorithm to increase our chances the much sought after relationship nirvana..
Stop after: $\lceil\frac{8}{e}\rceil = 3$.
That means that after my third relationship, I need to pick the one that is better than the highest of the three I have been through.
Looking at the facts:
- I am on my fourth relationship.
- It is quantitatively better than my previous three relationships.
Therefore, I have my answer.
To settle down with this person would be the mathematically optimal solution to my life partner problem.
This is the definition of romance.
In conclusion
Math. QED.
...
What? No.
What if this doesn’t work out?
What if everything you know is wrong?
You humans are too messy what with your non-deterministic emotions and all that. First of all, math is never wrong, you are wrong. Secondly we could easily tweak the variables to help those fragile emotions of yours.
Here are the parameters for the scenario I provided.
Starting age: 19
Stopping age: 35
Years per relationship: 2.5
Total relationships: 8
Optimal stopping number: 3
Say you just hit 30 and start dating as your full time job. Having one stable(?) relationship a month.
Total years: 10
Years per relationship: 0.1
Total relationships: 120
Optimal stop: 45
Maybe you’re swiping on the latest dating app Kindling or something, and you get 2 new matches a week. You’re probably going to continue this for a good 3 years before burning out.
Total years: 3
Years per relationship: 0.0096
Total relationships: 312
Optimal stop: 115
Whatever the case, I got you covered. I’ve coded a nifty little web app to help you with all your life choices. I was planning to make this all pretty and web 2019 eye candy like, but I’m not getting paid enough for this. You get a basic CSS thing.